一文彻底理解原码反码和补码
记得大学学计算机时,被这三个玩意折腾了很久,本人又是个钢铁直男,理解不透就没法继续,老师又只说记住就行了。
烦恼我许久,于是便整理了一下
直接开始吧
首先举个例子,通过这个例子来思考补码的意义
# 原码
咱们来算一下 (+6)+(-6)= 0
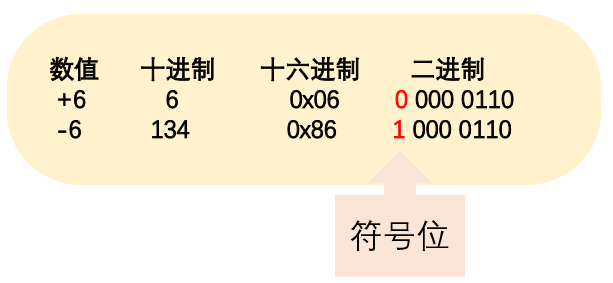
这个大家都可以理解
因为这个符号位,所以有这样
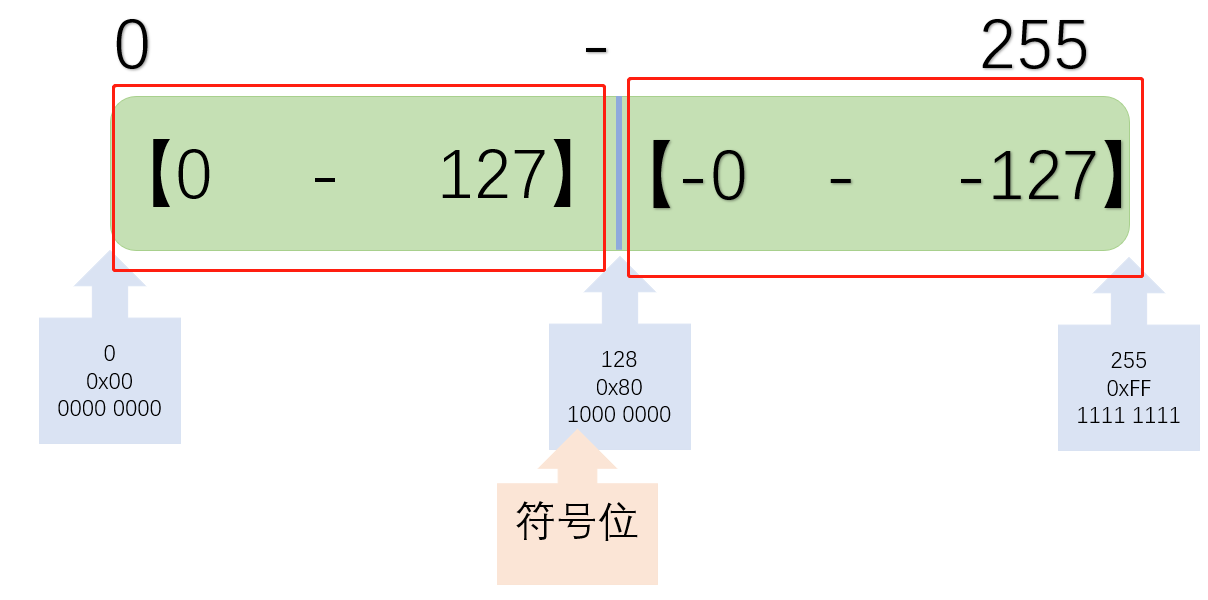
分成了两块
- 0-127
- (-0)-(-127)
这个时候(+6)+(-6)= (-12)
即:
0 000 0110
1 000 0110
=
1 000 1100(-12)显然错误
# 反码
正数 = 原码 负数 = 除符号位,其余按位取反
0 000 0110 =》 +6 【6】
1 111 1001 =》 -6 【249】
我们都知道(+6)+(-6)= 0,但是【6】+【249】=【255】
而【255:1111 1111 + 1 = 1 0000 0000】也算是等于零了,所以我们就是要想一个合理的办法凑出正确的答案
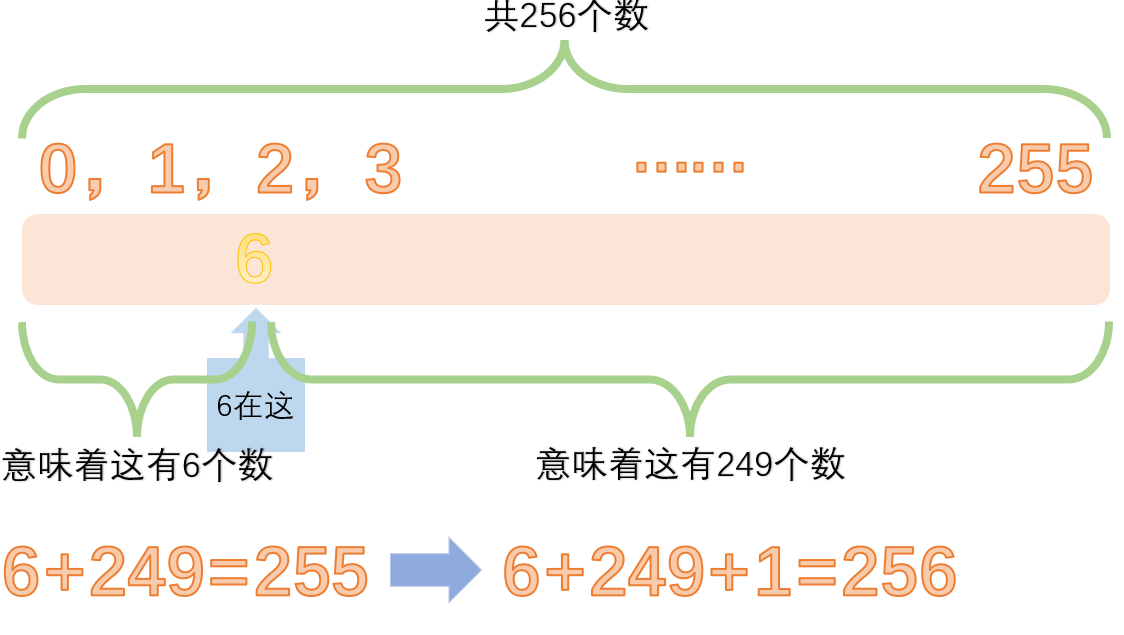
那么为什么要取反呢
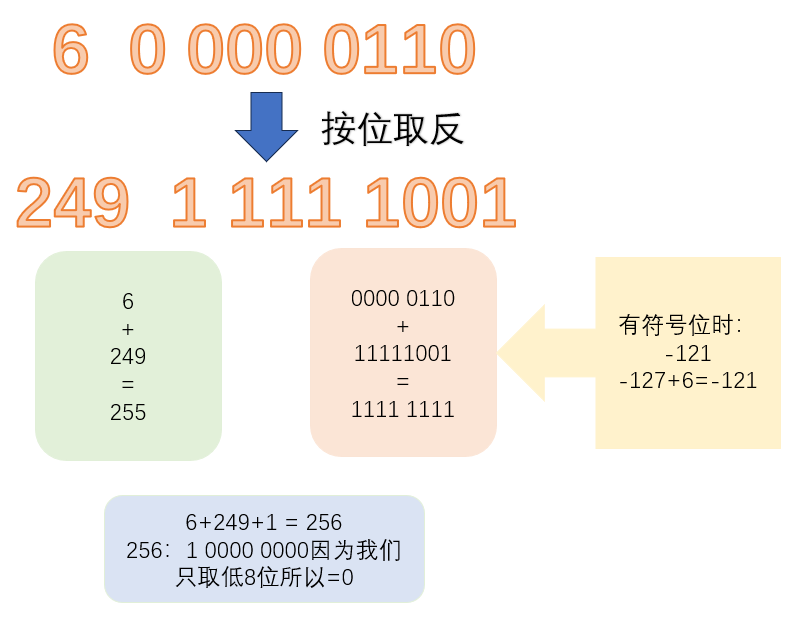
因为这个范围【0-127】【-0--127】
出现了 - 0,而事实上没有这个 - 0,所以负数运算时需要偏移 1 位。
正数 = 原码 负数 = 除符号位,其余按位取反。像这样的句子,本人是最烦背这个了😒
# 补码:
正数 = 原码 负数 =+1
有了上述的思考,那么这个补码就可以理解了吧!
0 000 0110 =》 +6
1 111 1010 =》 -6
# 意义:
有了这一系列的操作,终于明白补码的意义了吧。
就是为了解决计算机中的减法问题。
巧妙地把【减法】换算成了【加法】
那么为啥不直接用减法呢?
因为一位加法器实现:是用异或门来实现相加,与门来进位。
异或:^
可以参考
与:&
0&0=0
0&1=0
1&0=0
1&1=1
减法实现起来比加法器复杂不少,所以就只有加法就可以了。
